[Codeforces1013] Round #500 (Div. 2) [based on EJOI]

发表于 | 更新于 | 分类于 ， | 评论数： | 阅读次数：

链接：http://codeforces.com/contest/1013

A：n堆贝壳，第一天每一堆有ai个，现在可以拿走也可以移动任意个，然后给出第二天每一堆的贝壳的数量，问有没有可能。

两天的贝壳求和，如果不等就不可能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;

const int maxn = 1111;
int a, b;
int n;

signed main() {
  // freopen("in", "r", stdin);
  int t;
  while(~scanf("%d", &n)) {
    a = 0, b = 0;
    for(int i = 1; i <= n; i++) {
      scanf("%d", &t);
      a += t;
    }
    for(int i = 1; i <= n; i++) {
      scanf("%d" , &t);
      b += t;
    }
    if(a >= b) printf("Yes\n");
    else printf("No\n");
  }
  return 0;
}

B：给n个数ai，以及一个数x，现在允许x和ai进行与（&）操作后替换ai，问最少操作多少次，n个数中出现两个相同的数字。

由于和x进行与操作后的结果再和x进行操作的结果不会变，因此每一个数至多和x与1次。考虑到结果只可能是-1 0 1 2，因此存下与操作后的数字结果，讨论一下就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;

const int maxn = 100100;
int n, x;
int a[maxn];
int vis[maxn], vis1[maxn];

signed main() {
  // freopen("in", "r", stdin);
  while(~scanf("%d%d",&n,&x)) {
    memset(vis, 0, sizeof(vis));
    memset(vis1, 0, sizeof(vis1));
    int maxx = -1;
    for(int i = 1; i <= n; i++) {
      scanf("%d", &a[i]);
      maxx = max(maxx, a[i]);
      vis[a[i]]++;
      vis1[a[i]&x]++;
      maxx = max(maxx, a[i] & x);
    }
    int flag = 0;
    for(int i = 0; i <= maxx; i++) {
      if(vis[i] >= 2) {
        flag = 1;
        break;
      }
    }
    if(flag) {
      puts("0");
      continue;
    }
    flag = 0x7f7f7f7f;
    for(int i = 1; i <= n; i++) {
      if((a[i] & x) == a[i]) {
        if(vis1[a[i]] >= 2) flag = min(flag, 1);
      }
      else {
        if(vis1[a[i]]) flag = min(flag, 1);
      }
    }
    for(int i = 0; i <= maxx; i++) {
      if(vis1[i] >= 2 && !vis[i]) {
        flag = min(flag, 2);
      }
    }
    if(flag == 0x7f7f7f7f) {
      printf("-1\n");
      continue;
    }
    printf("%d\n", flag);
  }
  return 0;
}

C：给2n个数字，让你用这2n个数字构成n个二维平面上的点，要求是构造一个平行于坐标轴的、包括所有点的矩形，并且矩形面积最小（面积可以为0）。

很容易想到的是对a进行排序，之后将2n个数分为x坐标和y坐标两个集合，然后依次结合构成点。画图后发现答案就是两个集合的极差乘积，我们希望让这两个集合的极差尽可能小，因此每次从两个集合中拿出最小的放到对方的集合里，这里滑动窗口模拟一下就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;

using LL = unsigned long long;
const int maxn = 200100;
int n;
LL a[maxn];
pair<LL, LL> p[maxn];
map<LL, int> vis;
deque<LL> r, q;
multiset<LL> rr, qq;

signed main() {
  // freopen("in", "r", stdin);
  while(~scanf("%d",&n)) {
    vis.clear();
    for(int i = 1; i <= 2 * n; i++) {
      cin >> a[i];
      vis[a[i]]++;
    }
    sort(a+1, a+2*n+1);
    bool flag = 0;
    for(auto p : vis) {
      if(p.second >= n) {
        flag = 1;
        break;
      }
    }
    if(flag) {
      printf("0\n");
      continue;
    }
    r.clear(); q.clear();
    rr.clear(); qq.clear();
    LL x, y;
    for(int i = 1; i <= n; i++) {
      r.push_back(a[i]);
      rr.insert(a[i]);
    }
    for(int i = n+1; i <= 2*n; i++) {
      q.push_back(a[i]);
      qq.insert(a[i]);
    }
    LL ret = 9223372036854775800LL;
    for(int i = 1; i <= n; i++) {
      ret = min(ret, ((*rr.rbegin())-(*rr.begin()))*((*qq.rbegin())-(*qq.begin())));
      x = r.front(); y = q.front();
      r.push_back(y); q.push_back(x);
      r.pop_front(); q.pop_front();
      rr.erase(rr.lower_bound(x)), qq.erase(qq.lower_bound(y));
      rr.insert(y); qq.insert(x);
    }
    cout << ret << endl;
  }
  return 0;
}

D：要向一个n×m的矩阵里画叉，并且当三个叉构成如下图所示的操作：

img

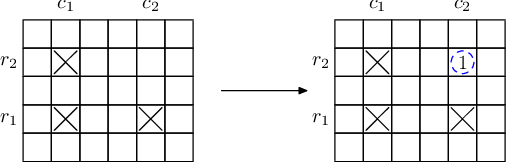
当到左图的情况时，会如右图：①的位置会补上（也就是构成了一个矩形）。

现在给你一个n×m的矩阵，以及一些画了叉的位置，问你最少需要手动画多少个叉，能够利用上述操作将整个矩阵填满。

考虑一个叉都不画的情况，最少需要画n+m-1（就是画一个十字）就能利用上述操作将矩阵填满。

再来考虑这个操作的实质：比方说现在有了(x1,y1)、(x1,y2)、(x2,y1)三个点，那么第四个点(x2,y2)实际上是没有贡献的，如下图：

img

转换成森林上，希望把坐标这个森林连成一片，问最少要加多少条边。这样我们读入数据的时候，x和y连起来（为了区别x和y，y+n来做分层），当他们的父亲不一样的时候，说明这个连接是必须有的，记一次数。之后用n+m-1减掉这个必要的计数就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pll;
const int maxn = 4000100;
int n, m, q;
int pre[maxn];

int find(int x) {
  return x == pre[x] ? x : pre[x] = find(pre[x]);
}

int unite(int x, int y) {
  x = find(x); y = find(y);
  if(x != y) {
    pre[x] = y;
    return 1;
  }
  return 0;
}

int main() {
  // freopen("in", "r", stdin);
  int x, y;
  while(~scanf("%d%d%d",&n,&m,&q)) {
    for(int i = 1; i <= n + m; i++) {
      pre[i] = i;
    }
    int cnt = 0;
    for(int i = 0; i < q; i++) {
      scanf("%d%d",&x,&y);
      if(unite(x, y+n)) cnt++;
    }
    printf("%d\n", n+m-1-cnt);
  }
  return 0;
}