[读书笔记] Neural Networks and Deep Learning Chapter 1

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

这是我阅读在线书籍《Neural Networks and Deep Learning》的笔记，这篇博文是第一章的。没什么营养，因为大部分都知道了，于是草草略过。

章节链接： http://neuralnetworksanddeeplearning.com/chap1.html

Introduction

科普。

words

  1. effortlessly：毫不费力地
  2. deceptive：欺骗性的
  3. superbly：雄伟地（文中表程度大）
  4. astoundingly：令人惊讶地
  5. stupendously：（同上）

科普。。

words

  1. morass：沼泽、困境
  2. caveats：警告

科普。。。讲下NN可以从一堆数据中学习到一些特征，然后去预测一些没见过的数据。并且数据越多效果越好。

介绍第一章要搞什么（手撸一个NN，用来识别手写数字，就74行），随后的章节要搞什么（想一些trick提升NN的acc之类）。

words

  1. intervention：介入、调停

手写数字识别这个问题简单，非常适合用来举例（大概这样可以把注意力更多地集中到NN本身之类？）。it’s challenging - it’s no small feat to recognize handwritten digits - but it’s not so difficult as to require an extremely complicated solution, or tremendous computational power.
(这是一项具有挑战性的工作——识别手写的数字绝非易事——但是拥有一个极其复杂的解决方案，或者是巨大的计算能力的话就不难了)，之后会讲一些扩展。

words

  1. throughout：自始至终

这章的重点：

两类神经元：感知机（Perceptrons）和sigmoid函数。

神经网络的标准训练方法：随机梯度下降（Stochastic gradient descent, SGD）

Amongst the payoffs, by the end of the chapter we’ll be in position to understand what deep learning is, and why it matters.最后会讨论一下DL为什么会matters。

Perceptrons

感知机（http://books.google.ca/books/about/Principles_of_neurodynamics.html?id=7FhRAAAAMAAJ）是一类人工神经元，由科学家Frank Rosenblatt在上世纪50到60年代间完成。

不过目前非常流行的一类模型是神经网络（Neural Network），最重要的一部分是sigmoid（就个非线性函数）。

img

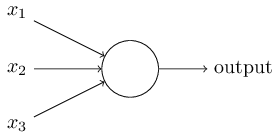
上图是个最原始感知机的神经元，嗯。

假设这个perceptron有三个输入$x_1,x_2,x_3$，中间的圈里一系列权重$w_1,w_2,w_3$。输入来的时候，我们首先做向量乘法$sum=\sum_i w_ix_i$，然后要和一个阈值$threshold$比较得到$output$：
$$
output=
\left{
\begin{array}{lll}
0, \ \ if\ sum \leq threshold \
1, \ \ otherwise.
\end{array}
\right.
$$

举个例子。

words

  1. transit：公共交通
  2. adore：崇拜、爱慕
  3. loathe：讨厌

img

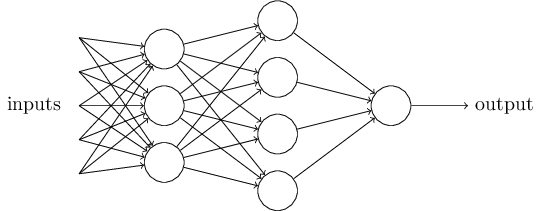
每一列称之为层（Layer），第一层的三个神经元对输入分别以自己的权重进行处理（每层的处理就是向量乘积，最后获得一个值），得到的输出（可能不用threshold判断）再分别给第二层的每一个神经元，第二层的决策会更加复杂，因为第二层的输入是通过第一层抽象过的结果。

实际上每个神经元的输入可以有很多，但是输出都是一个。这么画是为了说明层与层之间是如何联系起来的。

words

  1. plausible：可信的
  2. subtle：微妙的
  3. engage：从事，参与
  4. sophisticated：复杂的
  5. incidentally：顺便，附带地

把上述神经元的计算过程简化下：
$$
output=
\left{
\begin{array}{lll}
0, \ \ if\ \omega\cdot x+b \leq 0 \
1, \ \ otherwise.
\end{array}
\right.
$$
$b$就是bias，也是threshold。表示一种“输出1”的测量(the bias as a measure of how easy it is to get the perceptron to output a 1. )。

words

  1. cumbersome：冗杂的，累赘的
  2. notation：标志、符号、记号
  3. reminder：剩下的

举了个简单的例子，说明感知机可以做与、或、非之类的逻辑操作：

img

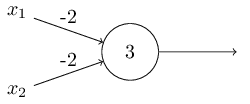
上图就是一个与非门，实际上感知机能做任何逻辑操作（因为这东西可以实现一切基本逻辑操作，那么就像连电路一样把那些门都连起来就行了）。

这是为了说明，感知机可以和其他计算设备一样强大。然而并非仅此而已，我们还可以在这个简单的模型上使用学习算法，使这个模型可以自己调整每一个神经元中的weights和bias，这种调节来自外部刺激（external stimuli），而非手动调整。

words

  1. equivalent：等价物
  2. notable：值得注意的

Sigmoid Neurons

先介绍更新权重的时候，可以表示成$\omega+\Delta\omega$的形式，这样就可以学习了（当然都是向量）。也就是，我们希望每次output反过头过来传个值，然后更新这个网络。

但是上述的naïve perceptron在输出的时候都会经过一个突变函数（非零即一），通过这个门以后后面的神经元就完全没法恒量差别了（就像雅思）。

引出sigmoid：

img

这里output为$\sigma(z) \equiv\dfrac{1}{1+e^{-z}}=\dfrac{1}{1+exp(-\sum_jw_jx_j-b)}$。

这样做的好处是对之前用的step function做了平滑处理，使得变化看起来不会过于激烈。看看原文是如何解释的：

The smoothness of $\sigma$ means that small changes $\Delta w_j$ in the weights and $\Delta b$ in the bias will produce a small change $\Delta output$ in the output from the neuron.

就是说变化后的w和b在处理完输入接着输出到output的时候，使得output的变化不至于太剧烈，output可以近似为下面的值：
$$
\Delta \mbox{output} \approx \sum_j \frac{\partial \, \mbox{output}}{\partial w_j}
\Delta w_j + \frac{\partial \, \mbox{output}}{\partial b} \Delta b
$$
确实可以用微分来解释，因为$\mbox{output}$是一个n元一次线性方程，那么对它微分就是各项偏导之和，而微分的几何意义就是表示偏移量（变化量）的。

我们需要有一个平滑函数$\sigma$来简化运算，由于指数在微分时的性质（无限可微），所以构造了sigmoid函数作为激活函数（sigmoid还有一个著名性质就是导数可以用自身表达）。

如何解释经过sigmoid的输出？

最大的不同是：经过sigmoid平滑后，输出由原来的0或1变为[0,1]中任意实数（希望变成0 1的话直接设阈值max一下就ok）。

words

  1. terrific：可怕的
  2. property：性质、性能
  3. occasionally：偶尔、偶然地、不定期地
  4. legitimate：合法的
  5. convention：约定

Exercises

part I：证明感知机中所有w、b都乘一个大于0的常数c，这个网络的输出不会改变。

证：$
\mbox{output}=
\left{
\begin{array}{lll}
0, \ \ if\ \omega\cdot x+b \leq 0 \
1, \ \ otherwise.
\end{array}
\right.$，乘一个整数不会影响。

part II：给一个感知机，对于任意输入$x$，都有$\omega\cdot x+b \not=0$。现在把所有神经元都替换成sigmoid神经元，再乘一个大于0的常数c，证明假如c趋于无穷大的时候，有sigmoid神经元的模型就会退化成没有sigmoid的网络。假如$\omega\cdot x+b =0$的时候又会有什么不同？

(1). 证：$c \to +\infty,c>0$时，可以分别将$lim$带入上述$\sigma$函数中求极限，发现分别收敛于0和1。

(2). 结果会输出0，而sigmoid会输出0.5，是不一样的。

The architecture of neural networks

img

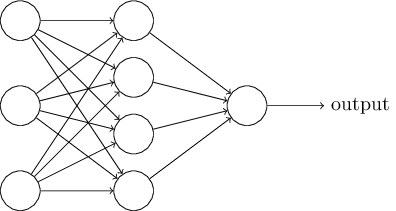
上图是一个网络，从左到右开始，第1层叫输入层（input layer），每个元素叫输入神经元；第2层叫隐层（hidden layer），未必只有一层；第3层叫输出层（output layer）。

img

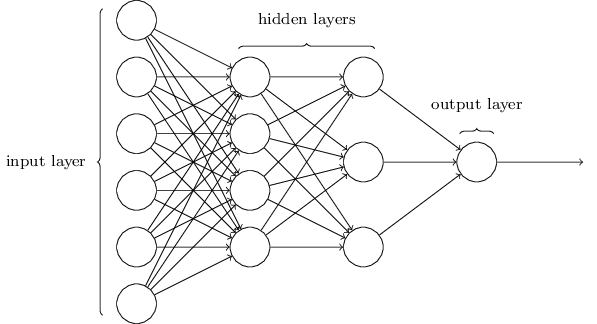
有多层的网络有时候也被称作“多层感知机”，这是有历史原因的。所以现在完全可以认为NN=MLP（MLP里的感知层（简单的线性操作）换成sigmoid）。

然后介绍识别手写数字的任务，提到最简单的构建NN的方法就是把一张图片（例如$64\times 64$）的灰度信息直接保存（输入直接是$4096$维，当然要把灰度归一化到[0,1]内），然后走一遍网络取argmax。同时，hidden layer的设计会非常多样。

前馈神经网络：通常定义只允许前面的层向后面的层输出，不允许反过来（不允许有环）。但是现在已经有一些可以带环的网络（RNN）。

words

  1. terminology：术语
  2. philosophical：哲学的
  3. rules of thumb：经验法则（大拇指规则）
  4. heuristics：启发、尝试（法）

A simple network to classify handwritten digits

本科做过了这段懒得读了。

img

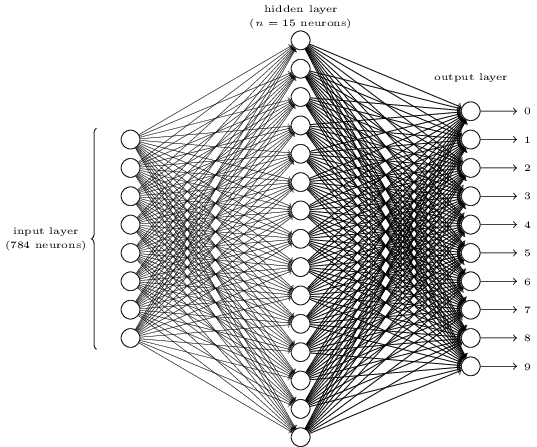
这个图挺帅，意思就是用一层hidden，然后输入是$28\times 28=784$维，然后最后输出10个分类的logits。

这里讨论了一个很有趣的问题：为什么输出是10个而不是4个（因为$2^4=16>10$可以表示所有我们希望的数字情况）？

个人认为隐层中每次处理后都会提取图像中的某一部分的特征，预测的时候被激活与否的影响因素为某部分是不是有这个特征，有某种特征对应0-9这十个数是很容易的，然而要对应二进制编码则很难表示。

words

  1. sake：利益、理由

Exercise懒得做了，只要对应好四个位置给权值就行了。

Learning with gradient descent

介绍mnist数据集，同时设计一些必要的环节：

$\mbox{cost function}$：$\begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x | y(x) - a|^2\end{eqnarray}.$（均方误差），训练过程中的目标是最小化$\mbox{cost function}$。

然后讲梯度下降：

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2. \end{eqnarray}$ 我们的目标是希望使$\Delta C$变负，$\Delta v_1,\Delta v_2$分别是两个不同方向的偏移量。因此可以说$\Delta C$是两个方向偏移量的叠加。

定义梯度向量：$\begin{eqnarray} \nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T. \end{eqnarray}$

所以化简后，变化量可以表示成：$\begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v. \end{eqnarray}$

定义$\begin{eqnarray} \Delta v = -\eta \nabla C\end{eqnarray}$，$\eta$是一个极小的正数（学习率），$\Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta |\nabla C|^2$，$\Delta C \leq0$恒成立知，$C$是一个只减不增的值，于是我们在算出的$\Delta C$（我们希望让$\Delta C$一直是负数，也就是$C$一直下降）的同时，算出$v$移动后的位置$v’=v-\eta \nabla C$。

img

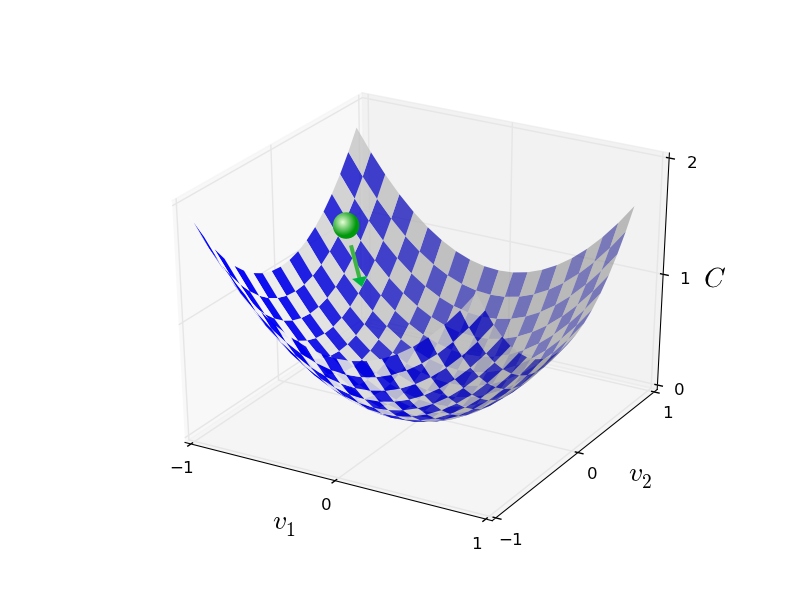
就像这个绿球一直往地势低的地方滚，直到最低点（极低点）为止。

到$m$维的向量空间，$\nabla C$的定义会得到扩展：
$$
\begin{eqnarray}
\nabla C \equiv \left(\frac{\partial C}{\partial v_1}, \ldots,
\frac{\partial C}{\partial v_m}\right)^T
\end{eqnarray}
$$
（对于$\Delta v$中的每维变量，都会有一个对应的梯度去更新它。）

通常训练神经网络的工作都是面对这样一个最优化问题，梯度下降算法可以看做是一个采用最少步骤使得$C$下降的一个方法。

words

  1. quadratic：二次的
  2. ah-doc：特别的
  3. recap：翻造、重申
  4. distract：转移、分心
  5. lurk：潜伏、埋伏、隐藏

Exercise

http://neuralnetworksanddeeplearning.com/chap1.html#exercises_647181

Part I. 证明上述的假设，即：当$\left|v\right| = \epsilon, \Delta v =-\eta \nabla C​$时，其中$\epsilon >0​$为很小的一个数，且当$\eta =\dfrac{\epsilon}{\left| \nabla C\right|}​$时，$\Delta C=\nabla C \cdot \Delta v​$可以取到最小值。（也就是要证给定步长，我们沿着梯度的方向总能找到最小值）

证明：当$\Delta C = \nabla C \cdot \Delta v$且$\left|v\right|=\epsilon$时，令$\Delta v=-\eta \nabla C=(-\epsilon/\left|\Delta C\right|)\nabla C$，则有：
$$
\begin{align}
\Delta C &= \nabla C \cdot \Delta v \
&= \nabla C \cdot ( -\epsilon/\left|\nabla C\right| ) \nabla C \
&= \nabla C ^2 ( -\epsilon/\left|\nabla C\right| ) \
&= \left|\nabla C\right| ^2 ( -\epsilon/\left|\nabla C\right| ) \
&= -\epsilon \left|\nabla C\right| \
&= -\left|\Delta v\right|\left|\nabla C\right|
\end{align}
$$
由柯西-施瓦兹不等式，$\left|u\right|\left|v\right| \ge \left|u \cdot v\right|$得，$\left|\Delta v\right|\left|\nabla C\right|\ge \left| \Delta v \cdot \nabla C \right|$，$-\left|\Delta v\right|\left|\nabla C\right|$必为最小值。

Part II. 给出一个在多维和一维情况下梯度下降的几何解释。

答：一维的话就退化成函数求导问题了，就是在一个曲线上找极小值，也就是一个圆点往地势低的地方滚。

接近物理学球下滚模拟的变种算法不可避免地需要求二阶偏微分，十分复杂。因此书中会引出一些方法来避免这个问题（梯度下降）。

梯度下降的目标是最小化$\mbox{cost function}\begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x | y(x) - a|^2 \nonumber\end{eqnarray}$.

反向更新的时候，这样来更新weights和biases：
$$
\begin{eqnarray}
w_k & \rightarrow & w_k’ = w_k-\eta \frac{\partial C}{\partial w_k} \
b_l & \rightarrow & b_l’ = b_l-\eta \frac{\partial C}{\partial b_l}.
\end{eqnarray}
$$
但是有一个问题，原始的梯度下降里，这个目标函数实际上是在求$C​$在不同$x​$取值时的均值，也就是要把整个dataset都迭代一遍后再去反向传播。

随机梯度下降（Stochastic gradient descent，SGD）每次选取指定规模的mini-batch去做梯度下降，在mini-batch的大小$m$满足：
$$
\begin{eqnarray}
\frac{\sum_{j=1}^m \nabla C_{X_{j}}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C,
\end{eqnarray}
$$
即$m$个输入的平均值要接近于全体输入的平均值，SGD才可近似于naïve GD。

1539092769209

带入权值和偏移更新中，公式变成这样：
$$
\begin{eqnarray}
w_k & \rightarrow & w_k’ = w_k-\frac{\eta}{m}
\sum_j \frac{\partial C_{X_j}}{\partial w_k} \
b_l & \rightarrow & b_l’ = b_l-\frac{\eta}{m}
\sum_j \frac{\partial C_{X_j}}{\partial b_l},
\end{eqnarray}
$$
在SGD时，称把整个数据集经过mini-batch训练一遍为一个epoch，通常要来好几个epoch。

在算目标函数的时候不要忘记$\frac{1}{n}$（用mini-batch的时候是$\frac{1}{m}$），做一下平均（因为有可能后来添加数据，就是说数据规模不一定的时候会影响到）。

words

  1. incidentally：顺便地，偶然一提地
  2. convention：惯例，约定
  3. omit：省略、疏忽

Exercise

提到了mini-batch size=1的时候的一种极限情况。

Implementing our network to classify digits

介绍数据集，和要实现的神经网络。稍微读下代码，其他没什么好看的。

Toward deep learning

又是一些废话。